|
|
|
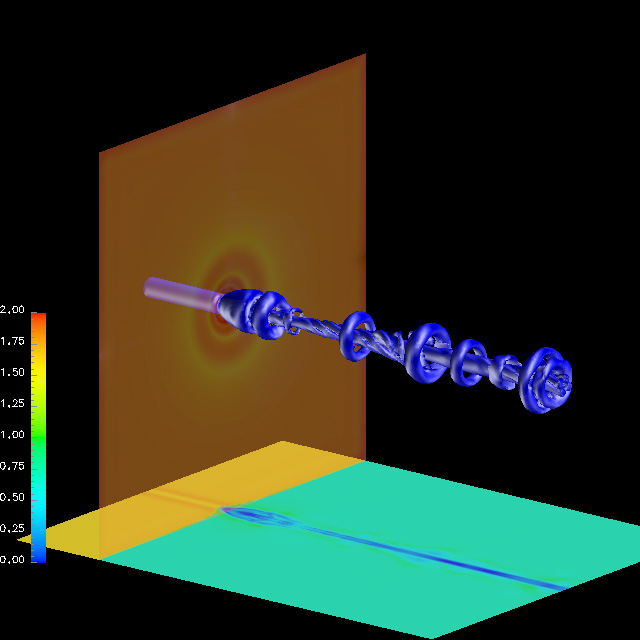
The picture shows vortex breakdown, enforced by the interaction of a normal
shock and a slender vortex with its axis parallel to the oncoming supersonic
flow. The phenomena was numerically simulated with a finite-volume solution
of the Navier-Stokes equations for time-dependent, compressible, viscous
flow. The conservation equations were written in divergence form, with
the time derivatives discretized with a Runge-Kutta five-step scheme,
and the spatial derivatives with a node-centered finite-volume technique.
A cartesian grid was used with clustering of grid points near the axis
of the vortex. The total number of grid points was 2 millions. Computations
were carried out for a free-stream Mach number Ma=1.6 and a Reynolds number
Re=15000, based on the initial vortex core radius. The inflow profile
of the azimuthal velocity component was prescribed by a BurgersŤ vortex
with the circulation Gamma=2.5, non-dimensionalized with the vortex core
radius and the stagnation speed of sound. The inflow profile for the axial
velocity component was assumed to be Gaussian with a velocity defect of
10 percent. The temperature distribution was computed from isentropic
relations. The figure shows the flow downstream from the normal shock,
visualized by the plane normal to the vortex. The breakdown process is
characterized by vortex shedding immediately downstream from the shock
and subsequent spiraling of the inner part of the core. The iso-surfaces
shown represent surfaces of constant pressure.
Contributed by Oliver Thomer, Aerodynamisches Institut der RWTH-Aachen
|
|