|
|
 |
2. Adding Wind Speed and Directions
When cycling in still air, you feel a wind that is caused by your own motion, and you feel it blowing directly in
your face at a speed equal to your own velocity. The wind you feel in the moving reference frame that is moving with the cyclist is known as
the "relative wind." If instead of cycling, you are standing still by the side of the road, you would feel no wind. The wind relative to a
stationary observer is known as the "absolute wind," which in still air would obviously be zero.
When cycling in a head wind, so that the wind blows in the direction directly opposite to your own
motion, the magnitude of the relative wind would be equal to the sum of your own speed and the absolute wind
speed. For a tail wind, the magnitude of relative wind would be equal to your own speed minus the absolute
wind speed.
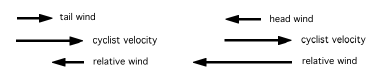 |
 |
Figure 2.1 Relative and absolute wind vectors for head and
tail winds. |
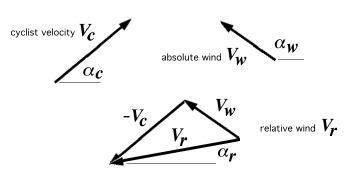
When cycling in a cross wind, we can use vectors. If \vec V_c is the velocity vector expressing the motion
of the cyclist (relative to a stationary observer), and if \vec V_w is the velocity vector expressing the
absolute wind (which is also relative to a stationary observer), then the relative wind vector \vec V_r
(that is, the wind speed and direction felt by the cyclist) is given by
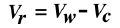
When cycling in a cross wind, there is also a relative wind direction. If \alpha_c is the direction of the
cyclist's motion (relative to a stationary observer), and if \alpha_w is the absolute wind direction
(which is also relative to a stationary observer), then the relative wind direction \alpha_r (that is, the
wind direction felt by the cyclist) is given by
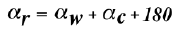
Note that both \vec V_r and \alpha_r depend on the speed of the cyclist.
 |
 |
Figure 2.2 Relative and absolute wind vectors for arbitrary
winds. |
|
 |